昨日ちょっと勉強のやり方について生徒に話したので、
それをここでもまとめておきたいと思います。
ちょっと抽象的なので、
文章だけでどこまで伝わるかわかりませんが、
とても大事なことです。
まず、勉強と言えばどう進めていくのが一番と感じていますか?
おそらく、1問ずつを完璧にしていくことを思い浮かべると思います。
例えばこのテキストの頭から順番にやって、
最初の1ページから完璧にやって、
それから次に進んでまた完璧にしていって。
そう考える人が多いと思います。
そのやり方が悪いとは言いませんし、
今から言うことを盾に基準を下げる人が出てきそうで怖いですが、
もっと良い方法があります。
まず最初のやり方で進めていったときに、
テキストの20ページくらいまで来たら、
最初1ページ目を忘れていませんか?
あんなに完璧にやったのに、
もう忘れてしまった!定期的に復習しないと!
って思いますよね?
確かにそうなんですが、
そのやり方だと一生そのままです。
だからテキストの前半部分って覚えている人が多いわけです。
気合いが違うのと、何回もやることになるからです。
ここからが本題です。
そうではなくて、
例えば塗り絵をするイメージを思い浮かべてみて、
丸の中の色を塗るとします。
その丸の中を最初から真っ赤に塗るのではなく、
薄くてもいいのでざっくりと塗る。
ざっくり塗るので塗る時間は短くて済みますよね?
それを何回も繰り返して、
そうしているうちに真っ赤にしていく感じです。
伝わりますかね?
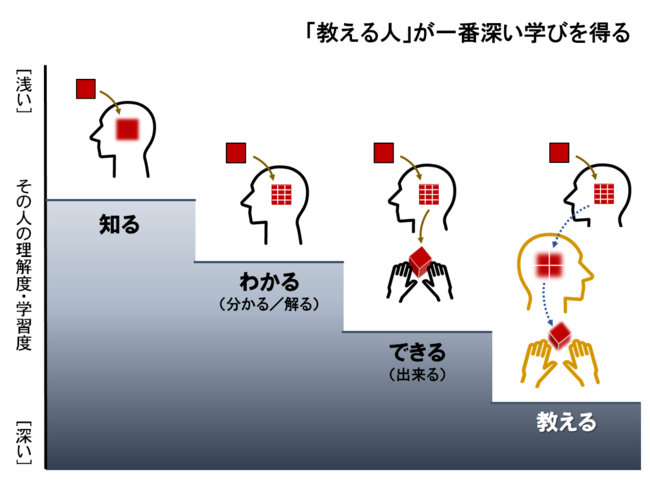
「問題を解けるようになる」ためには
「分かった」のレベルを上げていかなければいけない。
皆さんが分かったというものにはレベルがあります。
言葉にすると、
・知る
・分かる
・できる
・教える
この4段階です。
基準が低いと言われるのは、
この段階の「知る」や「分かる」で止まっている場合です。
「できる」にまで到達して初めて70点を超えてきます。
「できる」まで到達して70点です。
教えるまで行って初めて80点を超えてきます。
後はその「教える」の精度を上げていけば100点にどんどん近づいていくわけです。
分かるの段階
ちょっと下がっていくグラフになっているのでわかりにくいですが、
下がるほどにできるようになるというグラフです。
そしてその「できる」や「教える」になるまでに、
一気にその地点に到達することをせずに、
「知る」をたくさん繰り返してくださいという話です。
1問に対して、一気に「教える」まで行くのではなく、
「知る」を繰り返していくうちに自然と「分かる」になり、
「分かる」を繰り返していくうちに自然と「できる」になり、
「できる」を繰り返していくうちに自然と「教える」になり、
「教える」を繰り返していくうちに自然と「完璧」になっていきます。
これが一番成績が伸びます。
ではテキストを実際どうやったらいいのかです。
一番わかりやすいのが英単語なので、それで説明します。
例えば目の前に英単語1900が載っている単語帳があるとします。
ページにすると100ページくらいだと思います。
それを4日でこなしてください。
1日25ページです。
その時に、見て5秒後に答えられたらOKとしてください。
だからサクサク進むはずです。
最初はそれで構いません。
そして4日で終わらせてください。
終わったらまた最初から繰り返しです。
また4日で終わらせてください。
それをずっとやり続けてください。
丸を赤く塗るように、
薄い赤から真っ赤になるまで何度もやってください。
それは人によって違うと思います。
5回やれば覚える人もいるでしょうし、
100回やってもまだ足りない人もいるでしょう。
でもできるまでやり続けることが大事なことは皆さんご存じのとおりです。
だからできるまでやってください。
英単語に限った話ではなく、
国語も社会も理科も数学も同じです。
だからワークを何周もするし、
同じテキストも何周もするわけです。
これで少しは同じ問題を何周もする意義が伝わったでしょうか?
ここに同じ問題を何周もする大義があるわけです。
上の方でも書きましたが、
基準を下げてよいという話ではありません。
とにかく人に教えられるまで極めてください。
何度も何度も繰り返してください。
数学なら例題を暗記して問題文まで暗唱できるレベルに。
社会は記述問題の答えから問題文を作成できるレベルに。
理科は出した数値から計算問題を作成できるレベルに
英語は一つの文の精読の解説ができるレベルに。
国語はすべての文を暗記して、その文を別の言葉で言い換えられるレベルに。
そこまでやれば向かうところ敵なしになります。
全国模試で1位と聞くとかっこいいと思うわけですよね?
なれる可能性は全員にあります。
後はこれを実行するかどうかです。
結局最後はそこに集約されます。
言われたことをやるかやらないか。
やる人が2割です。
だから行動力のある人が強いんです。
毎日塾に来てそういう勉強をしているから、
栄進研に通っている生徒でも素直に指示を守る子は強いわけです。
めんどくさくてやらないから伸びない。
差はそういう所でしか逆に生まれません。
とにかく行動!それが一番です。
\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\
全国の敏腕塾長が集まり本を出版します!
本では語りつくせなかったことや、本の内容をもっと知りたいなどの質問を受け付ける
オープンチャット「全国敏腕塾長に質問!」も用意しております。
LINEアカウントはこちら
ホームページのお問い合わせはこちら


